

 )
就有 4x4x4=64 個不同的三張牌的組合。
每一色由123到789有七款順子,三色合起來就共有 7x3=21 款順子。
整副麻雀裏,共有 64x21=1344 個三張牌的順子組合。
)
就有 4x4x4=64 個不同的三張牌的組合。
每一色由123到789有七款順子,三色合起來就共有 7x3=21 款順子。
整副麻雀裏,共有 64x21=1344 個三張牌的順子組合。不少現代雀迷,看過古典麻雀的介紹,會有一個壞的第一印象。 驟眼看來,古典麻雀很「畸形」:「混一色」與番牌同樣只值一番, 副點既難計又看似沒什麼道理,「莊家么二制」裏莊家雙計但又不問放銃責任, 驟眼看來有太多的問題。
實不相瞞,筆者起初接觸古典麻雀時,第一印象也不是好得到那裏去。 但是經過了長時間的研究與思索,我才領悟到,原來那不好的第一印象, 是受了現代麻雀「先入為主」的觀念(成見)的影響, 要客觀地分析古典麻雀,就要拋開成見,不要從現代麻雀的角度去批評, 而是從古典麻雀的角度去理解。
現代麻雀主要是按「和種」去計番,但是在古典麻雀裏, 所謂和種只是一個客串的角色,只是間中加少少分數, 遇到特別漂亮的牌(一色系)才加一番或三番。 古典麻雀章法的主角,就是刻、槓的副點,與及番牌的一番。 不單是和了牌就可以按刻、槓加副,而是每一手牌都會按刻、槓算副, 按副點向其他三家(或兩家,因為和牌者有免疫權)收取。 這些副點,就是古典麻雀章法的基本及中心。
古典麻雀不以和種為章法的中心,是因為那是原始的章法,當時麻雀剛剛面世,
和種中心的造牌概念還未發展成熟,所以自然地就以最直覺的方法來計分;
古典章法的中心,不是衡量整手牌一貫的美感的和種,
而是逐個面子來衡量難度的副點。
只有刻、槓計副,順子一律算 0副,這樣合理嗎?
我們可以用科學的方法分析,數學中有一門叫「組合數學」(Combinatorics),
即是「數東西的捷徑」,組合數學在「或然率」(Probability)、
「博奕學」(Game Theory) 裏有很大實用價值。
對於組合數學認識較少的讀者,請見附錄乙,
在那處我會解釋以下所用的
一個順子由三張數牌構成,因為一副牌裏每款牌有四張,所以每款順子
(例如 

 )
就有 4x4x4=64 個不同的三張牌的組合。
每一色由123到789有七款順子,三色合起來就共有 7x3=21 款順子。
整副麻雀裏,共有 64x21=1344 個三張牌的順子組合。
)
就有 4x4x4=64 個不同的三張牌的組合。
每一色由123到789有七款順子,三色合起來就共有 7x3=21 款順子。
整副麻雀裏,共有 64x21=1344 個三張牌的順子組合。
一個刻子由三張相同的牌組成,從四張同款牌中取三張,
共有
算一算,就發覺麻雀牌裏,順子的數目約為刻子的10倍。 就算考慮到順子只可以靠摸牌或「吃」上家,刻子則可以靠摸牌或「碰」三家, 這也只是 2:4(即 1:2)之比,合起來刻子還是比順子難很多。 所以古典麻雀裏順子算 0副,只有刻子加副,是完全合乎數理的。
槓子比刻子難,暗刻、暗槓又各比明刻、明槓難,所以副點較多, 這也是合理。但是為什麼么九的點數要比中張牌高呢?么九的刻子, 本身並不會比中張牌的刻子難造,問題是各牌的「面子組成效率」。
所謂「面子組成效率」,即是某一張牌,要與另外兩張牌組成面子時,
能發揮多少效用,我們就數這張牌能組成幾多組面子。
每款順子,另外兩張牌有 4x4=16 個組合,而每款刻子則只有
效率最好的,是三到七的中張牌,每張可以構成三款順子及一款刻子, 相當於9款刻子的效率。其次是二八牌,每張可以構成二款順子及一款刻子, 相當於6.33款刻子的效率。
么九牌只能構成一款順子及一款刻子,相當於3.66款刻子的效率, 只有中張牌的四成。所以作為對使用這些低效率牌的獎勵, 么九牌的刻、槓有雙倍副點,這是合理的。至於字牌,由於不能組成順子, 所以就只有1款刻子的效率,因此不止值雙倍副點,還有加番。 把字牌分為三元牌(公將)與風牌(門將),這樣可增加遊戲的特色與趣味。
古典麻雀裏,混一色只得一番,與現代麻雀一般的三番比較起來, 給人一個明顯是太少的感覺。與古典麻雀的其他一番和種,例如番牌、 平和等比較,混一色明顯是難度高很多,看來應該不止值一番。 另外,由四副升值到一番的對對和也有同樣問題,不要說四副, 就算一番也是嫌太少。
其實,在早期的古典麻雀裏,混一色的一番是恰當,不是太少。 我們首先要明白,古典麻雀不是以和種為中心的造牌麻雀, 章法的中心是刻、槓的副點,對和種不太重視,所以和種的數目很有限, 分值也偏低。番牌的一番,可以說是副點系統的一個伸延,與副點同樣, 和不到牌也可以計這一番,嚴格來說,番牌不算「和種」,所以不應該拿去跟和種比較。 至於平和等,古典麻雀初期原本是沒有平和的 (或者應該說,平和像「雞和」般只是一個叫法,不是有價值的和種; 請見「平和論」), 所以真正的問題不在於混一色值一番是太少,而是在於後來平和等增值到一番, 變得與混一色一樣,實在是太多了。
至於對對和,其實四副也是合理,因為每個刻、槓本身已有副點, 所以不用特別加很大的獎勵給對對和。 與其他的四副和種比較,對對和也不見得比它們難。
我們要明白,古典麻雀主要是以計刻、槓的副點為中心,和種只是一個配角, 撇開了滿貫和種不算,和種就以第9類的和牌形式類為主。 今日的新章和種,會以手牌各方面的一貫性與系統性為理據, 但當時就只有清一色系列與對對和。 前者可以說是眾多和種之中理據最明顯的,而後者則是副點的自然、當然的伸展: 既然每一個刻、槓都值副點,那麼全手牌都是刻、槓,自然也值得加多幾副。 試想想,中庸裏的新章和種,例如「一般高」、「三色同順」、「一氣通貫」等, 這些和種的理據概念一點也不難,不是什麼高深的學問,如果說要編一些麻雀的和種, 應該不難想到這些。古典麻雀沒有這些和種,原因不是作者想不出這些和種, 而是作者根本沒有很努力地去想可以有哪些和種,因為古典麻雀是計副點的麻雀, 和種只是配角,沒有大做文章的必要。初期的加番和種只有清一色與混一色, 是因為古典麻雀把一色手牌視為「例外」的特別漂亮的手牌,所以加番獎勵; 要注意「例外」這二字,古典麻雀沒有「起和」,所以一色手牌視為特別例外的手牌, 只有當拿到很好的一色配牌時才會去造,不像三番起和的舊章般, 把混一色當為家常便飯,「不理三七二十一」,局局都去造混一色。
古典麻雀的授受法,規定了莊家的收支加倍, 卻不計較放銃責任(包牌的特殊情形除外)。這樣公平嗎?
莊家的雙計,是因為有著重莊家的概念,規則規定是這樣,也沒有什麼公平不公平的。 問題是放銃責任,尤其是打慣了今日流行的(所謂)「全銃」制度的雀迷, 可能會覺得,對於無辜被拖累的兩家好像不公平。
古典麻雀也不是沒有放銃責任的概念,在九張等包牌的情形下, 放銃者還是要包付三家。那麼為什麼不從第一天起就乾脆用「全銃制」? 要解答這個問題,就要從理解古典麻雀的概念與動機入手。
古典麻雀的遊戲目的,是很單純的:各家鬥快去造成面子, 造成刻子或槓子便可得分,順子比較容易所以無分數, 但只要完成四面子加一對眼的(基本)和牌形便可以和牌,可以獲得副底及享有免疫權。 遊戲的主要目的是完成面子與和牌形,是一個「得分」的遊戲,和牌者一家贏牌, 其他三家便同視作輸家,所以便各自付錢給贏家。 這是古典麻雀原本的概念,所以不應該去問為什麼古典麻雀不用全銃制, 反而應該來問為什麼現代麻雀採用了全銃制,並思考全銃制的動機與利弊。¹
古典麻雀章法,按難度等加副給刻、槓,符合了數學的原理,在這方面設立了一個好的榜樣。 雖然這是很原始的章法,只有最少限的和種,不及「中庸」等的現代造牌麻雀的技術性及好玩程度, 但以一個原始的計副章法來說,是一套很妥當的章法,設計得相當不錯。
後來的造牌麻雀,參考了「一色系」的理據概念(即手牌的一貫性與系統性)發展出更多的和種, 亦(多少)遵從數學原理按和種的難度等來調整番值。 古典麻雀雖然原始、有限,但已局部地提示了造牌麻雀的理想概念。
中庸計分法採用新章和種,並以和種取代了刻、槓副點來做章法的中心。 除了這兩點以外,中庸的許多規則都是以古典規則為依歸。
為什麼要這樣做?是為了尊重麻雀的原作者的意圖。 有關麻雀原作者的身份,是一個眾說紛紜的謎題,但是我們可以透過古典章法, 看到編撰這套章法的人的意圖及理念。 雖說此「古典初期」章法未必一定是「麻雀」最初的規則, 編撰這套古典章法者未必是麻雀的「原作者」,但他的確把麻雀章法整理妥當, 此章法亦成為後世各大章法的基礎,在麻雀史上立了一個里程碑, 所以他就算不是麻雀的第一原作者,也可以算是第二作者, 遵照他的意圖來發展麻雀規則,是合情合理。
以古典規則為依歸的,包括「中庸競技制」這授受法、廢除場風、 以「跟張免責規條」來取代諸多禁例、加算法、和種的分類及複合規則等,未能盡列。
有些人可能會這樣想:一款刻子有
筆者同意槓子比刻子難,所以槓子應值較高的副點,但是上述的1比4的算法,其中實有謬誤。 問題是刻子的4個組合是三張牌的組合,槓子的1個組合卻是四張牌的組合,牌的張數不同, 所以不能把組合數這樣拿來比較。否則的話,九蓮寶燈的聽牌形有 4^9x3=786432 個十三張牌的組合, 暗槓則只有34個四張牌的組合,你說那一個難?
粗略地算,暗槓的機會約為暗刻的 1/12。實戰裏槓子的頻度也好像 沒有刻子的 1/4。
運用組合數學時,常常會遇到各樣的陷阱,所以必須要小心想清楚。 (希望本書裏的數學沒有計錯吧!)
看第二章的麻雀列表,字牌類和種有大三元與四喜和, 但卻偏偏沒有「字一色」,這看起來有點怪。
如果把字一色當作「清一色」來算三番,加至少一番的番牌(因為字牌裏無番的就只有三個客風, 所以字一色的四刻字牌裏,就必定至少有一刻番牌)即至少四番。 副底10副,四個字牌刻子計16副以上,對對和4副,番牌對子2副,聽牌形2副,合計34副以上, 四番即544副以上,夠滿貫有突了。
牌例(南家和牌):
碰:

 碰:
碰:

 碰:
碰:


 銃和:
銃和:


 | 4副 |
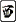 | 4副 |
 | 4副 |
 | 4副 |
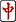 | 2副 |
| 對對和 | 4副 |
| 雙碰和 | 2副 |
| 副底 | 10副 |
| 34副 | |
| 清一色 | (3番) x8 |
 | (1番) x2 |
| 544副 |
古典麻雀的原作者,到底是忽略了「字一色」這個明顯的滿貫和種, 還是因為知道必定是「數滿貫」所以有意省略,這點筆者也無從得知。
© 2009 Alan KWAN Shiu Ho